A Focus Article titled "New Phase Space Formulations and Quantum Dynamics Approaches" by the Jian Liu group of the College of Chemistry and Molecular Engineering, Peking University, was published in Wiley Interdisciplinary Reviews Computational Molecular Science on May 13, 2022.
In the framework of Newton's classical mechanics, all physicochemical properties of molecular systems can be described on phase space consisting of coordinate and momentum variables. Real time dynamics is depicted by the classical trajectory on phase space. However, nature is in principle governed by quantum mechanics. When quantum characteristics of a molecular system becomes important, Heisenberg’s uncertainty principle implies that the coordinate and momentum of a particle cannot be simultaneously determined, where classical mechanics fails.
In 1932, Eugene Wigner (the Nobel Laureate in Physics in 1963) proposed the phase space formulation as an equivalent interpretation of quantum mechanics. He established a one-to-one correspondence relationship between quantum operators and coordinate-momentum phase space functions. In the coordinate-momentum phase space formulation, it is convenient to bridge the quantum and classical concepts as well as to develop practical trajectory-based approximate dynamics approaches for large molecular systems.
Since the difference between the mass of an electron and that of a nucleus is at least three orders of magnitude, the celebrated Born-Oppenheimer (BO) approximation assumes that the electronic and nuclear motions are well-separated. In the BO scheme, the adiabatic electronic states are obtained when the coordinates of nuclei are fixed. The potential energy surface (PES) for the relevant adiabatic electronic state is then produced either in advance or on-the-fly as nuclear dynamics is considered. The BO approximation is, however, not valid in nonadiabatic dynamics that occurs in many important quantum mechanical phenomena, such as photochemistry, electron transport/transfer, and cavity-modified transition processes in chemical, materials, biological, and environmental molecular systems. Nonadiabatic dynamics includes quantum mechanical behavior of both electrons and nuclei.
Because a typical molecular system has vibrational, rotational, and translational motion, it is often much more convenient to employ continuous coordinate space rather than Hilbert space with dense states to describe nuclear degrees of freedom (DOFs). On the other hand, the energy gap between different electronic states of interest is often significantly larger such that the (adiabatic or diabatic) state representation is more useful to depict electronic DOFs. It is evident that a general description of the molecular system leads to a composite quantum system, especially in the nonadiabatic region, where nuclear DOFs are described by continuous variables and electronic states are represented by discrete variables.
When the BO approximation is valid, the molecular system is denoted as the adiabatic system. The coordinate-momentum phase space formulation of quantum mechanics has shown its advantages in capturing nuclear quantum effects that become important in molecular systems at low temperatures or containing light atoms (hydrogen, helium, or lithium). The well-known linearized semiclassical initial value representation (LSC-IVR) is equivalent to the quasi-classical dynamics with quantum statistics on Wigner phase space. It satisfies the three important limits: classical limit, high temperature limit and harmonic limit. Recently developed quantum dynamics methods on Wigner phase space, equilibrium continuum dynamics (ECD) and path integral Liouville dynamics (PILD), are capable of satisfying the three important limits as well as conserving the quantum Boltzmann equilibrium distribution during the evolution. They provide more accurate approaches for simulating complex molecular systems at a given temperature. Phase space quantum dynamics methods have been applied to (infrared and Raman) vibrational spectra of gas phase molecules (water, ammonia, methane, formaldehyde, hydrogen peroxide, etc.), and liquid water in the condensed phase. By employing machine learning techniques, it is shown that the computational efficiency of the phase space quantum dynamics method can be significantly improved. This makes it practical to study nuclear quantum effects of larger molecular systems.
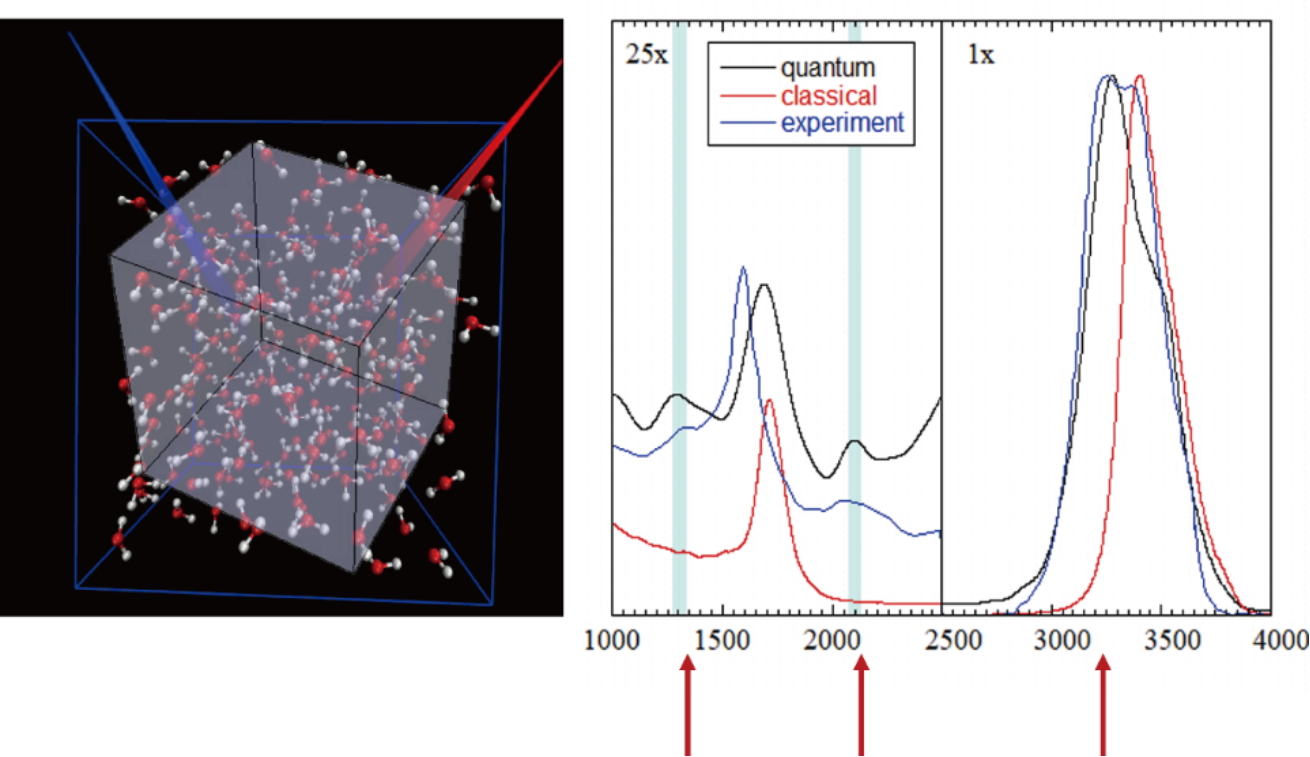
Fig. 1 Simulation of Raman vibrational spectra of liquid water by trajectory-based dynamics method on Wigner phase space.
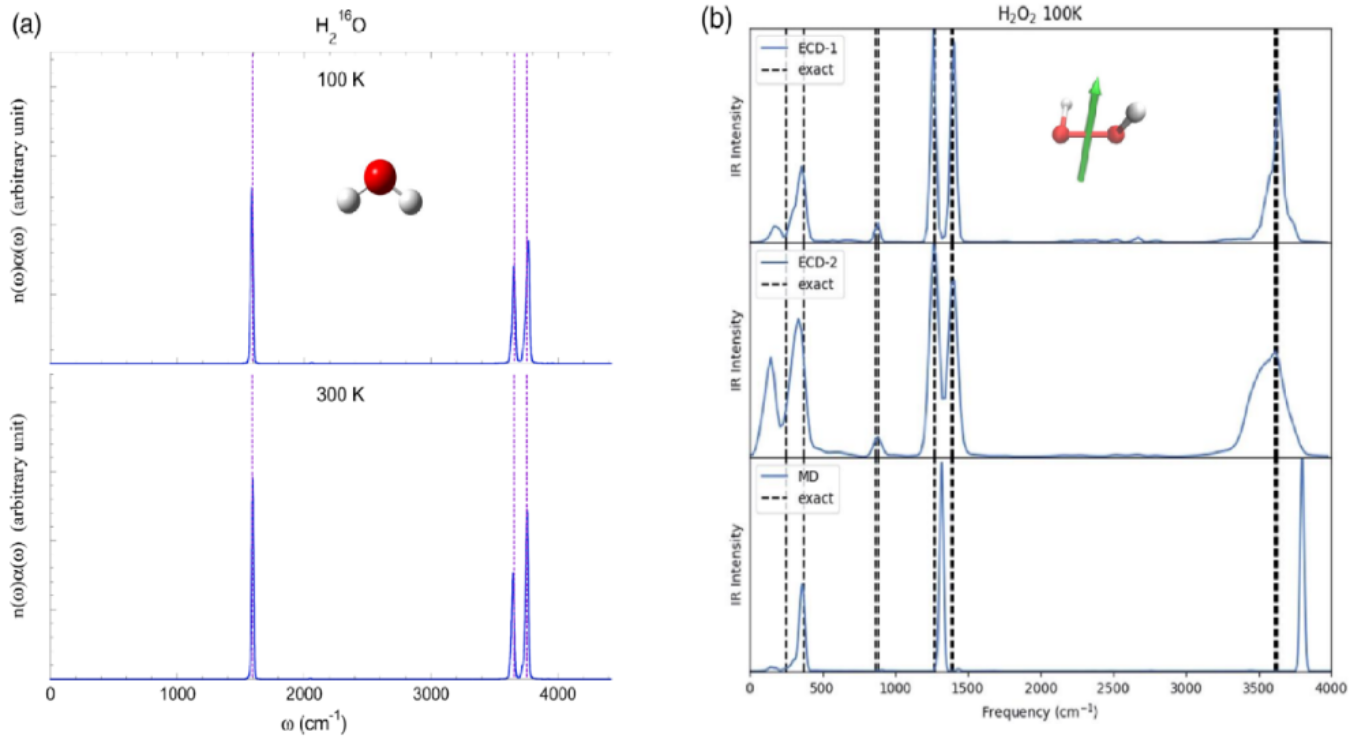
Fig. 2 Simulation of infrared spectra of water / hydrogen peroxide molecules by trajectory-based dynamics on Wigner phase space.
When the BO approximation breaks down, a molecular system involves the non-radiative transition between electronic states, where nuclear and electronic motion is coupled. Such a system is denoted as a nonadiabatic system, which is in principle a composite quantum system. This is typical in various photochemical and photophysical processes (such as photosynthesis, photoisomerization, photocatalysis, excited state proton transfer, electron transfer reaction, electronic energy transfer, carrier transport, singlet fission, etc.). Because the conventional coordinate-momentum phase space representation with the infinite boundary is useful only for the continuous-variable system, it is necessary to establish the theory of exactly mapping discrete variables onto coordinate-momentum phase space such that a generalized formulation is available for studying nonadiabatic systems on coordinate-momentum phase space.
Based on the unified framework of mapping Hamiltonian models developed in 2016, the Liu group first proposed in 2019 that the physical requirement that the total population of electronic states is always one should be used as a constraint for developing trajectory-based nonadiabatic dynamics. A phase space mapping dynamics approach was developed in J. Chem. Phys. 2019, 151, 024105. The formalism was extended to a generalized constraint (coordinate-momentum) phase space representation of the discrete-variable quantum system consisting of a finite number of quantum states. When the constraint coordinate-momentum phase space representation is used for electronic DOFs and the Wigner phase space representation is employed for nuclear DOFs, we have an exact formulation of any quantum properties of nonadiabatic systems.
When the equations of motion governed by the mapping Hamiltonian is used to approximate the quantum Liouville equation (or generalized Moyal equation) on mapping phase space, the nonadiabatic dynamics approach is denoted as the classical mapping model (CMM). In the Focus Article, the constraint coordinate-momentum phase space formulation is generalized to the weighted constraint phase space formulation. The mapping Hamiltonian dynamics is denoted as the weighted mapping model (wMM) approach for nonadiabatic dynamics. In addition that the (weighted) constraint coordinate-momentum phase space representation is useful for the visualization of quantum (entangled) states (Fig. 3), the trajectory-based nonadiabatic dynamics methods on mapping phase space (CMM and wMM) outperform prevailingly used Ehrenfest dynamics and fewest-switches surface hopping (FSSH) approaches for nonadiabatic dynamics (Fig. 4).
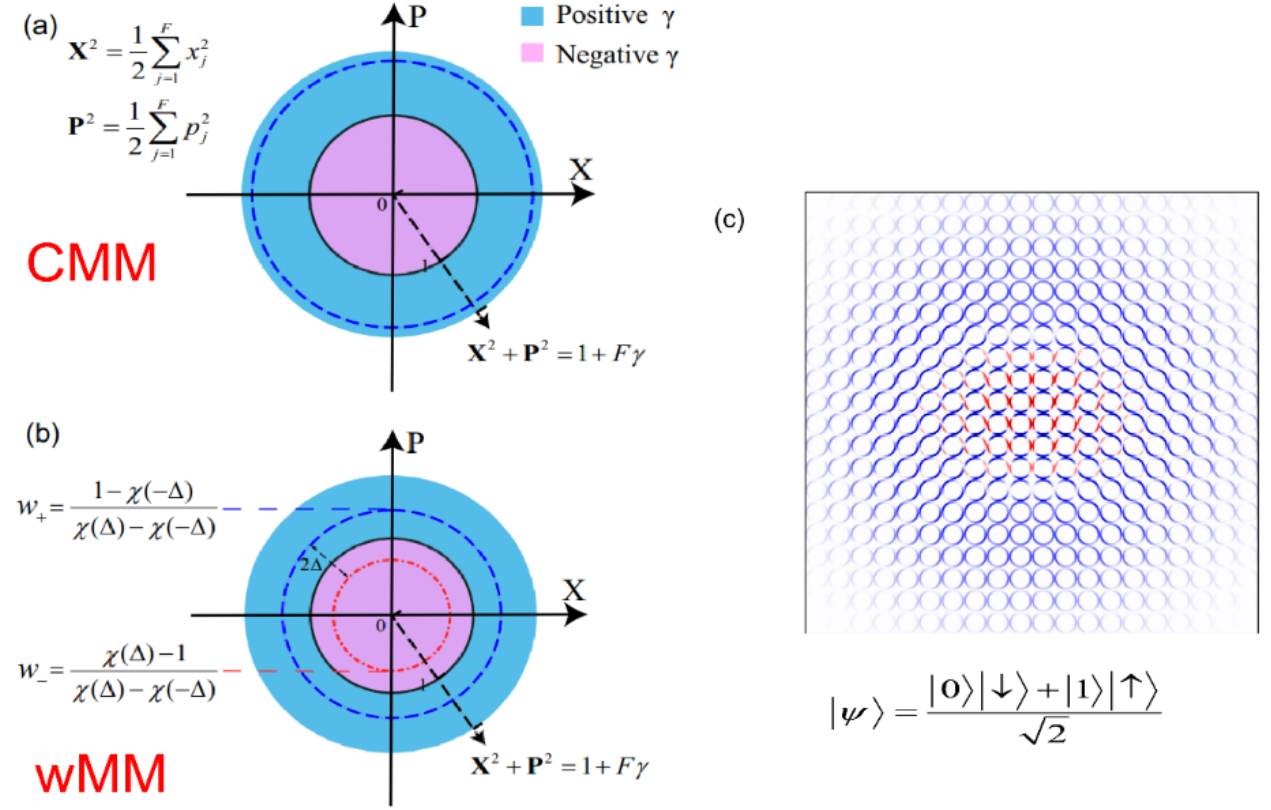
Fig. 3 Panels (a, b) are schematic representations of (weighted) constraint coordinate-momentum phase space for electronic DOFs. Panel (c) is an illustration for the mapping phase space of a composite system, of which Wigner phase space is used for nuclear DOFs and weighted constraint phase space is employed for electronic DOFs.
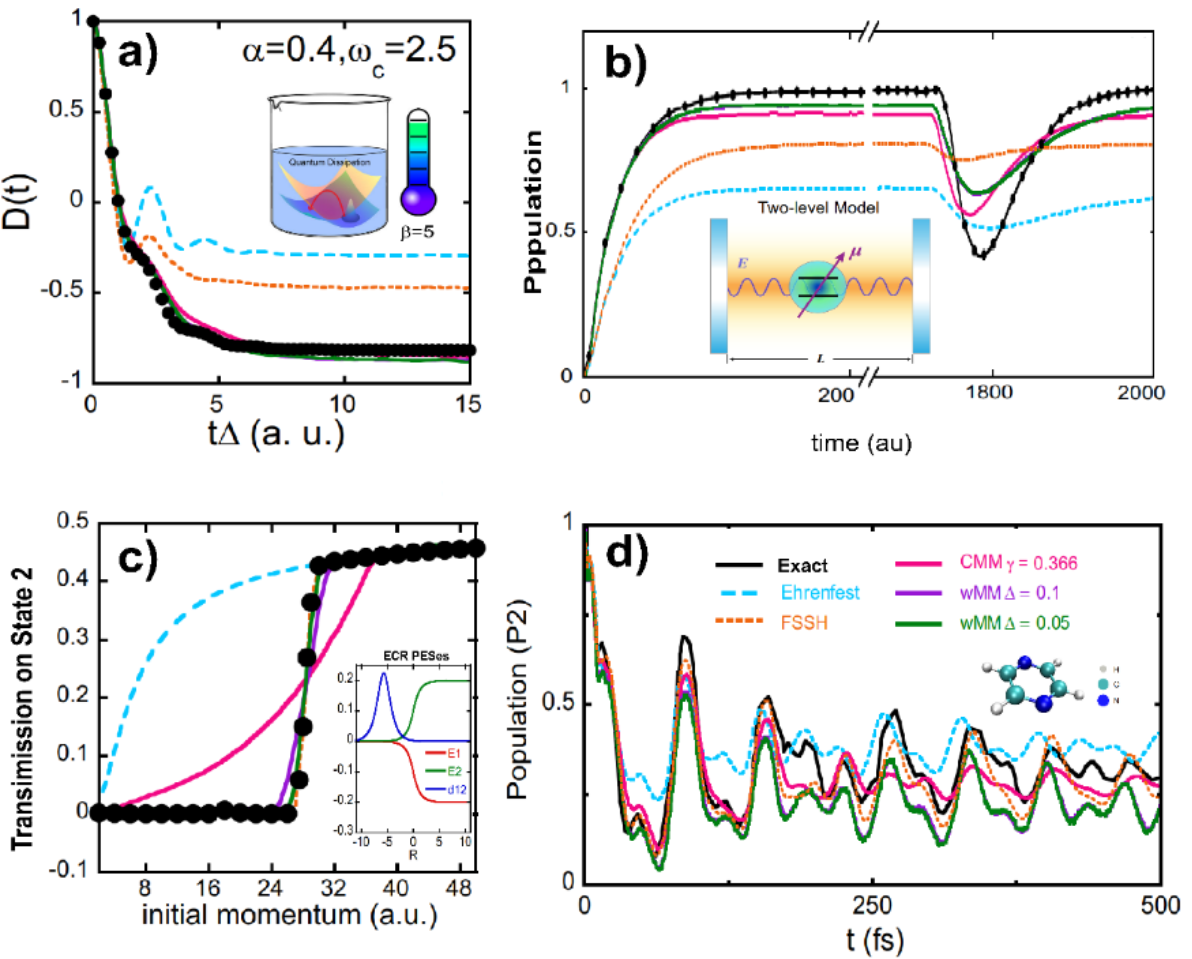
Fig. 4 Numerical performances of CMM and wMM in a series of benchmark nonadiabatic problems. Panels (a), (b), (c), and (d) demonstrate the results of the spin-boson model, atom-in-cavity model, Tully's ECR model and pyrazine’s conical intersection model, respectively.
In the Focus Article, the Liu group also review the relation between the equations of motion in the adiabatic representation and those in the diabatic representation, the relation between constrained coordinate-momentum phase space and Stratonovich SU(F)/U(F-1) phase space, the derivation of the equations of motion of the Meyer-Miller mapping Hamiltonian on mapping phase space, the relation between the mapping Hamiltonian dynamics and the quantum Liouville equation in the generalized coordinate-momentum phase space representation, and so forth.
To summarize, the Liu group has developed a generalized coordinate-momentum phase space formulation and proposed trajectory-based quantum dynamics methods for molecular systems where the B-O approximation is valid as well as for those where electronic and nuclear equations of motion are coupled. It is expected that the phase space mapping theory and dynamics approaches will be useful for studying vibrational as well as photochemical dynamic processes of complex molecular systems in the condensed phase.
The Focus Article is an invited contribution to Wiley Interdisciplinary Reviews Computational Molecular Science (Founded in 2011, the 2021 impact factor is 25.113). Xin He and Baihua Wu are the co-first authors. Prof. Jian Liu is the corresponding author. Other coworkers include Youhao Shang, Bingqi Li, and Xiangsong Cheng. The work was supported by the National Natural Science Foundation of China, Ministry of Science and Technology of China, Beijing National Laboratory for Molecular Sciences, and College of Chemistry and Molecular Engineering of Peking University. It was also supported by the High-performance Computing Platform of Peking University, Beijing PARATERA Tech CO., Ltd., and Guangzhou supercomputer center for providing computational resources.
Paper Information
New Phase Space Formulations and Quantum Dynamics Approaches.
Xin He#, Baihua Wu#, Youhao Shang, Bingqi Li, Xiangsong Cheng, Jian Liu*.
Wiley Interdisciplinary Reviews Computational Molecular Science, 2022, e1619
https://doi.org/10.1002/wcms.1619
and its Supporting Information
https://wires.onlinelibrary.wiley.com/action/downloadSupplement?doi=10.1002/wcms.1619&file=wcms1619-sup-0001-Appendix+S1.pdf
Other related article:
Jian Liu*, Xin He, Baihua Wu, Accounts of Chemical Research, 2021, 54, 23, 4215–4228 https://doi.org/10.1021/acs.accounts.1c00511